一、概念
互质关系
如果两个整数(或者两个以上的整数)的最大公约数是1,则称他们为互质。也就是说两个整数,除了1以外,没有其它的最大公约数了,这两个整数就叫做互质关系。
比如说7,11他们的最大公约数只有1,所以他们互质;8,10他们的最大公约数为1,2,所以这两数不是互质关系。
欧拉函数
欧拉函数φ(n)是小于或等于n的正整数中与n互质的数的数目,称为欧拉函数
比如说当n=8时,与8能形成互质关系的数有4个,分别是1,3,5,7,所以φ(8)=4
具体φ(n)函数的计算公式,可以分为以下四种情况:
情况一: 当n=1,φ(1)=1
因为1与任何整数都是互质关系,所以当n=1时,φ(1)=1
情况二:当n为质数,φ(n)=n-1
因为质数与小于它的每一个数,都构成互质关系,所以当n为质数时,φ(n)=n-1 。
比如说n=3时,1,2都跟他是互质关系, n=7时,1,2,3,4,5,6都跟他是互质关系。
情况三:n = p^k (p为质数,k为指数,且大于等于1),n是质数的k次方,则φ(p^k) = p^k - p^(k-1) = p^k(1 - 1/p)
比如:φ(8) = φ(2^3) = 2^3 - 2^2 = 4
φ(27) = φ(3^3) = 3^3(1 - 1/3) = 18
情况四: n是两个互质的整数之积,如:n = p1 * p1,则 φ(n) = φ(p1p2) = φ(p1)φ(p2)
比如:φ(56)=φ(8×7)=φ(8)×φ(7)=4×6=24
二、定理
同余定理
给定一个正整数n,如果两个整数a和b满足a-b能够被n整除,即(a-b)/n得到一个整数,那么就称整数a与b对模n同余,记作a≡b(mod n)。这就是同余定理。
例如:26≡2(mod 12), 26%12 余2, 2%12余2, 26-2/12 = 0,所以26与2对模12同余
欧拉定理
在数论中,欧拉定理是一个关于同余的性质。欧拉定理表明,若n,a为正整数,且n,a互素(即 ),则
),则

即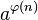 与1在模n下同余;
与1在模n下同余; 为欧拉函数。
为欧拉函数。
首先看一个基本的例子。令a = 3,n = 5,这两个数是互素的。比5小的正整数中与5互素的数有1、2、3和4,所以 。计算:
。计算: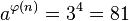 ,而
,而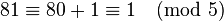 。与定理结果相符。
。与定理结果相符。
这个定理可以用来简化幂的模运算。比如计算 的个位数,实际是求
的个位数,实际是求 被10除的余数。7和10互素,且
被10除的余数。7和10互素,且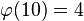 。由欧拉定理知
。由欧拉定理知 。所以
。所以  //欧拉函数φ(n)的作用就是把ap表示成aφ(n)*x+y
//欧拉函数φ(n)的作用就是把ap表示成aφ(n)*x+y
一般地,在简化幂的模运算的时候,(当a和n互素) 我们要对a的指数取模 :
:
当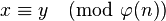 ,则
,则 。
。
三、求欧拉函数
一、直接法
原理:
Euler函数表达通式:euler(x)=x(1-1/p1)(1-1/p2)(1-1/p3)(1-1/p4)…(1-1/pn),其中p1,p2……pn为x的所有素因数,x是不为0的整数。euler(1)=1(唯一和1互质的数就是1本身)。
//直接法 int euler(int n) { int res=n,a=n; for(int i=2;i*i<=a;i++) { if(a%i==0) { res=res/i*(i-1); while(a%i==0) a=a/i; } } if(a>1) res=res/a*(a-1); return res; }
二、欧拉筛选法
void euler(int n) { phi[1]=1;//1要特判 for (int i=2;i<=n;i++) { if (flag[i]==0)//这代表i是质数 { prime[++num]=i; phi[i]=i-1; } for (int j=1;j<=num&&prime[j]*i<=n;j++)//经典的欧拉筛写法 { flag[i*prime[j]]=1;//先把这个合数标记掉 if (i%prime[j]==0) { phi[i*prime[j]]=phi[i]*prime[j];//若prime[j]是i的质因子,则根据计算公式,i已经包括i*prime[j]的所有质因子 break;//经典欧拉筛的核心语句,这样能保证每个数只会被自己最小的因子筛掉一次 } else phi[i*prime[j]]=phi[i]*phi[prime[j]];//利用了欧拉函数是个积性函数的性质 } } }
三、另一种更简洁的筛选法、推荐
const int maxn = 1e6+10; int prim[maxn], w[maxn], cnt = 0;//prim[i]起标记作用,prim[i]==0表示i是质数,注意这里把1也标记成了质数 int x[maxn];//x[i]表示偶数是i的符合条件的两个质数是x[i]和i-x[i]; void init() { memset(prim, false, sizeof(prim)); prim[1]=1;//1不是素数 for(int i = 2; i < maxn; i++) { if(prim[i]) //判断i是否为偶数 continue; w[cnt++] = i;//w存质数 for(int j = i << 1; j < maxn; j+=i)//把所有质数的倍数标记 prim[j] = true; } }
欧拉公式的延伸:小于n的且与n互质的数的和是euler(n)*n/2
来源:CSDN
原文:https://blog.csdn.net/u012861385/article/details/24271435
來源:简书