更改了一下程序的错误。
Translation
找出凸包,然后逆时针输出每个点,测试数据中没有相邻的边是共线的。多测。
Solution
首先推销一下作者的笔记 由此进入>>> (
明显是一道二维凸包模板。
在这里,我们简单讲一下二维凸包。
「
在平面上能包含所有给定点的最小凸多边形叫做凸包。
其定义为:对于给定集合 (X) ,所有包含 (X) 的凸集的交集 (S) 被称为 (X) 的 凸包 。
(qquadqquad) —— OI-Wiki
」
其实我们可以把凸包看成一个拿橡皮筋围成的一个图形。
假设有一个布满小凸起的板子:

我们要把这些凸起都围起来,怎么围呢?
显然,最简单方变的方法是这样:
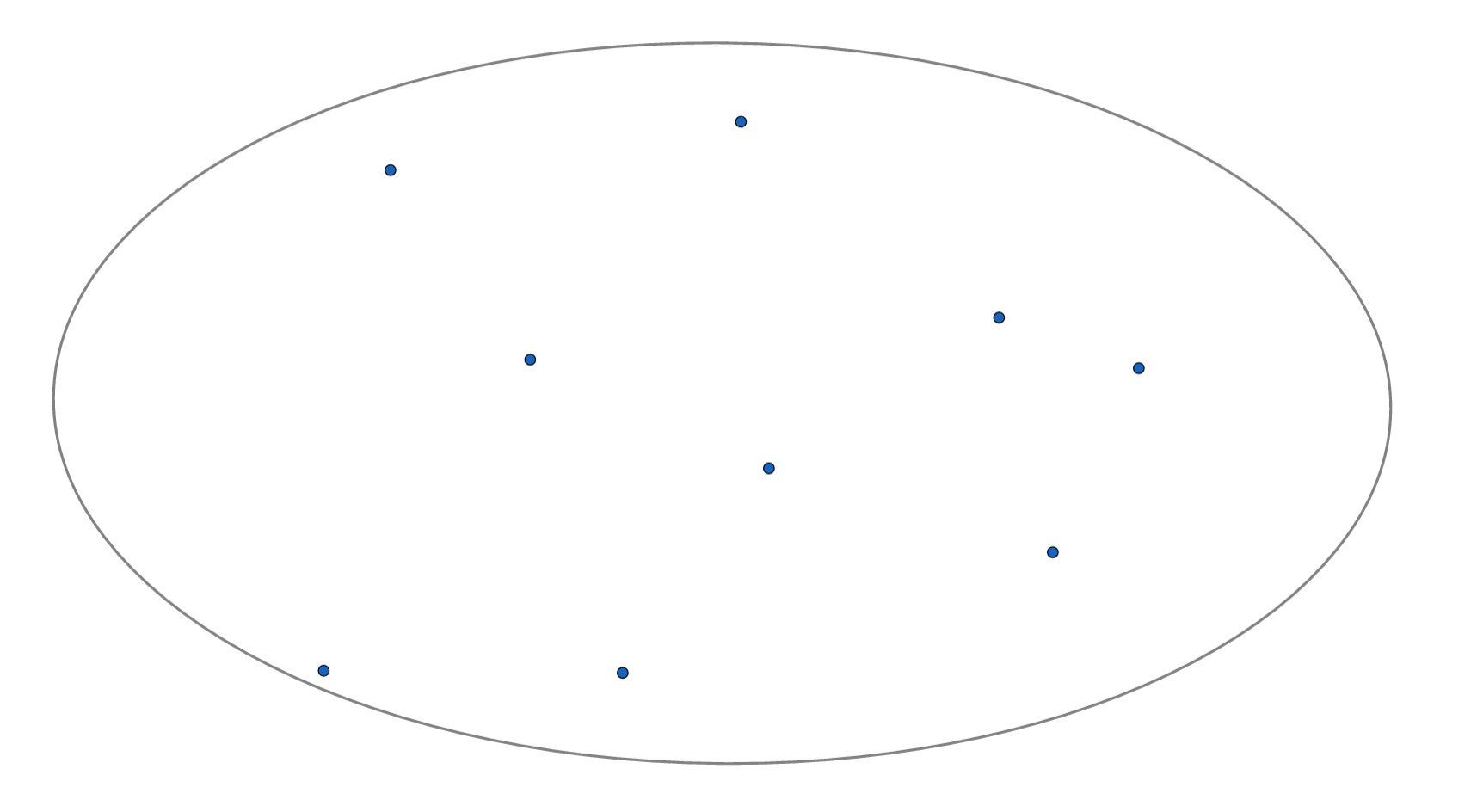
但是,我们知道,橡皮筋是有弹力的,所以橡皮筋会往里缩,直到这样:
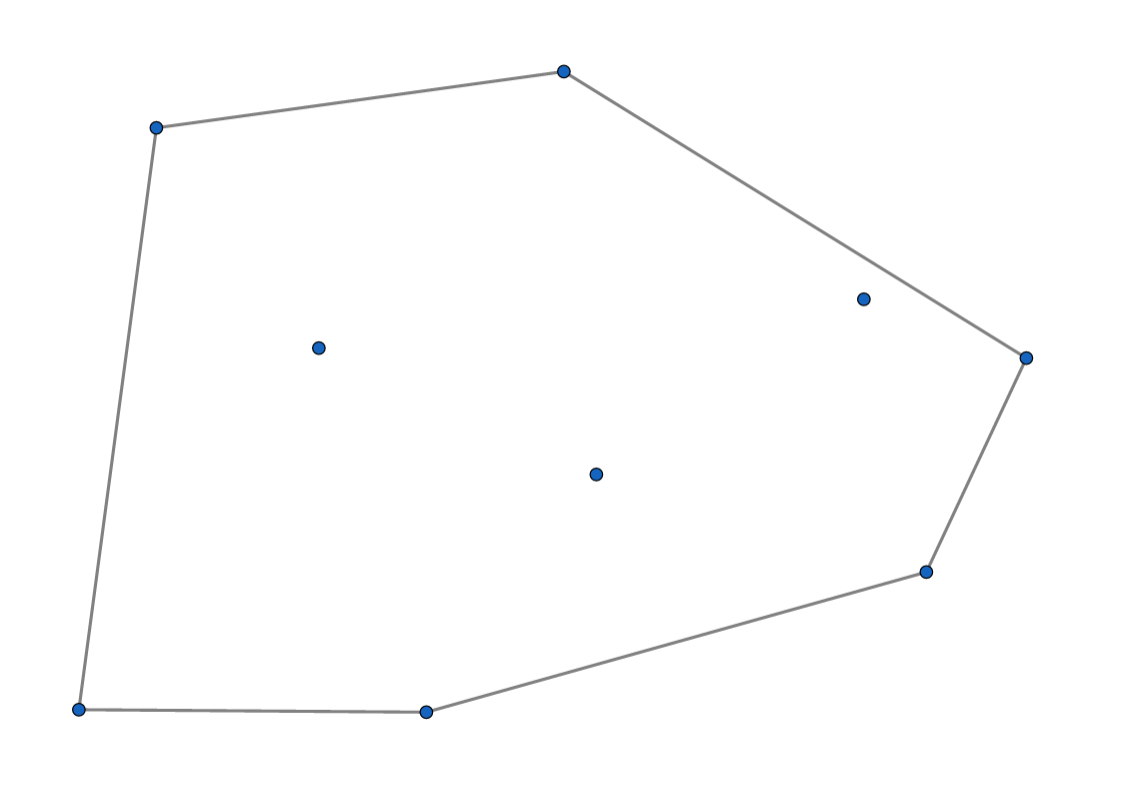
最外圈的凸起撑起了橡皮筋。
此时橡皮筋围成的多边形的顶点就是最外圈凸起所在的位置。
由此,我们就定义橡皮筋围成的图形为一个平面凸包。
那么,换一种定义,就为:
平面凸包是指覆盖平面上 (n) 个点的最小的凸多边形。
当然,我们发现在程序中却无法模拟橡皮筋收缩的过程,于是有了下文的诞生。
二维凸包的求法
斜率逼近法
其实这也是一种容易想到的算法,但是并不常用(代码复杂度高),所以我们省略带过。
Jarvis 算法
这其实是一种数学构造法
此算法的时间复杂度为 (O(nm))。
但是,这个复杂度会爆炸。
于是我们伟大的 (sf OIer) 就想到了 Graham 算法。
Graham 算法
Graham 算法的本质:
Graham 扫描算法维护一个凸壳,通过不断在凸壳中加入新的点和去除影响凸性的点,最后形成凸包。
凸壳:凸包的一部分。
此算法主要分为两部分:
- 排序
- 扫描
排序
我们先选择一个 (y) 最小的点(如 (y) 相同选 (x) 最小),记为 (p_1)。
剩下的点,按照极角的大小逆时针排序,记为 (p_1,p_2,dots, p_m)。
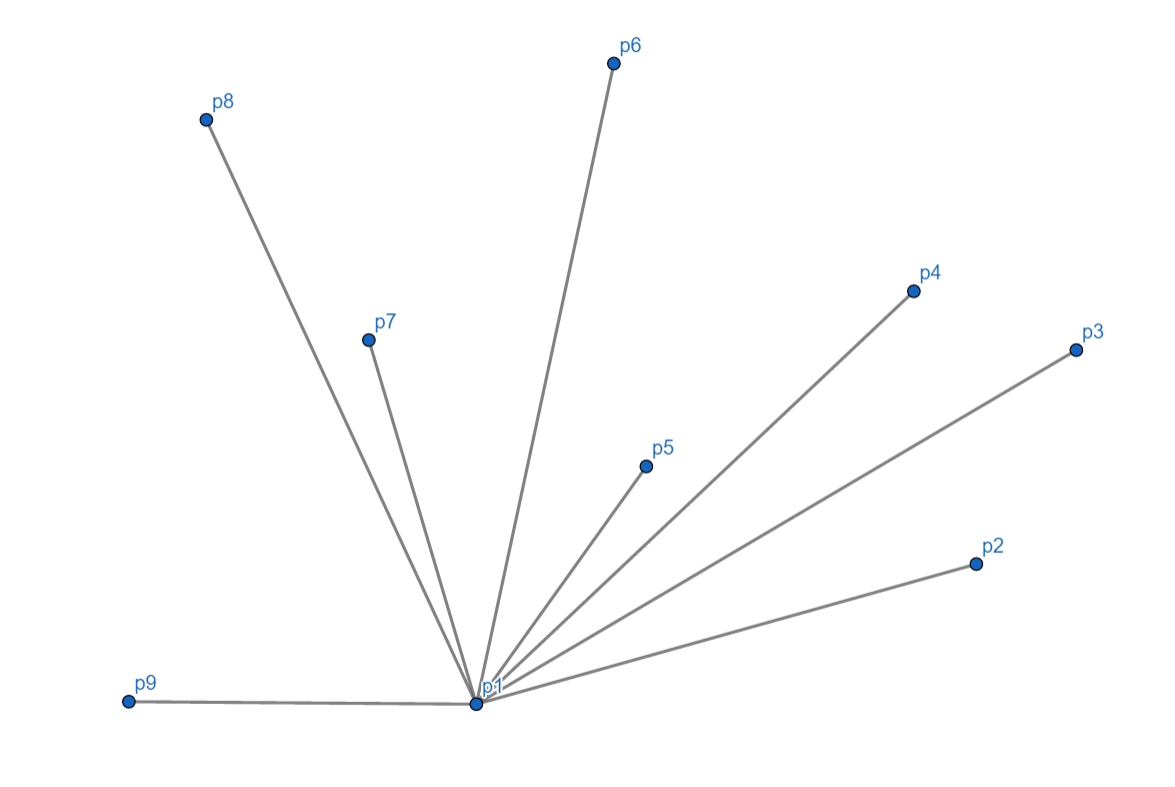
我们按照排序结束时的顺序枚举每一个点,依次连线,这里可以使用一个栈来存储,每次入栈,如果即将入栈的元素与栈顶两个元素所构成了一个类似于凹壳的东西,那么显然处于顶点的那个点一定不在这个点集的凸包上,而他正好在栈顶,所以把它弹出栈,新点入栈。
扫描
(下列所说的左右等是指以上一条连线为铅垂线,新的连线偏移的方向)
刚开始,我们的点集是这样的:

(p_1) 为起始点。
随后,(p_2) 准备入栈,由于栈元素很少,所以可以入栈。
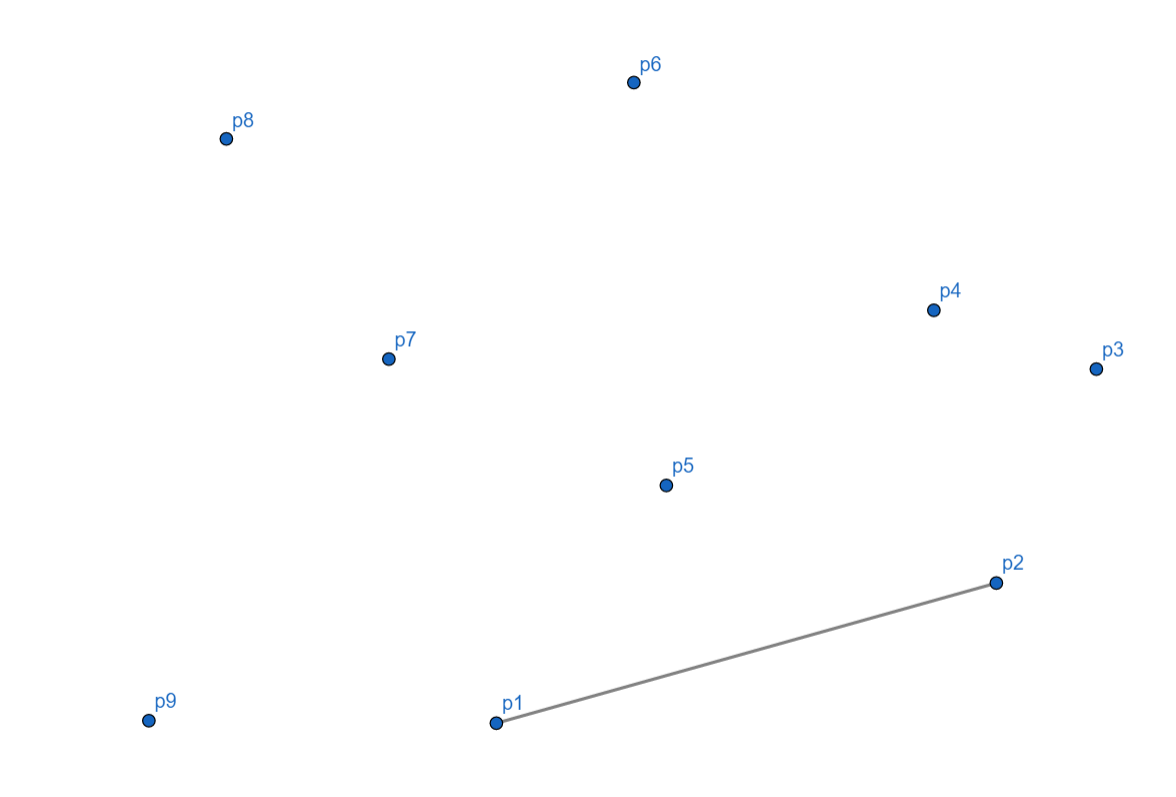
再看 (p_3),因为 (p_3) 向左,符合凸包条件,入栈。

随后 (p_4) 也一切正常,依然向左,入栈。
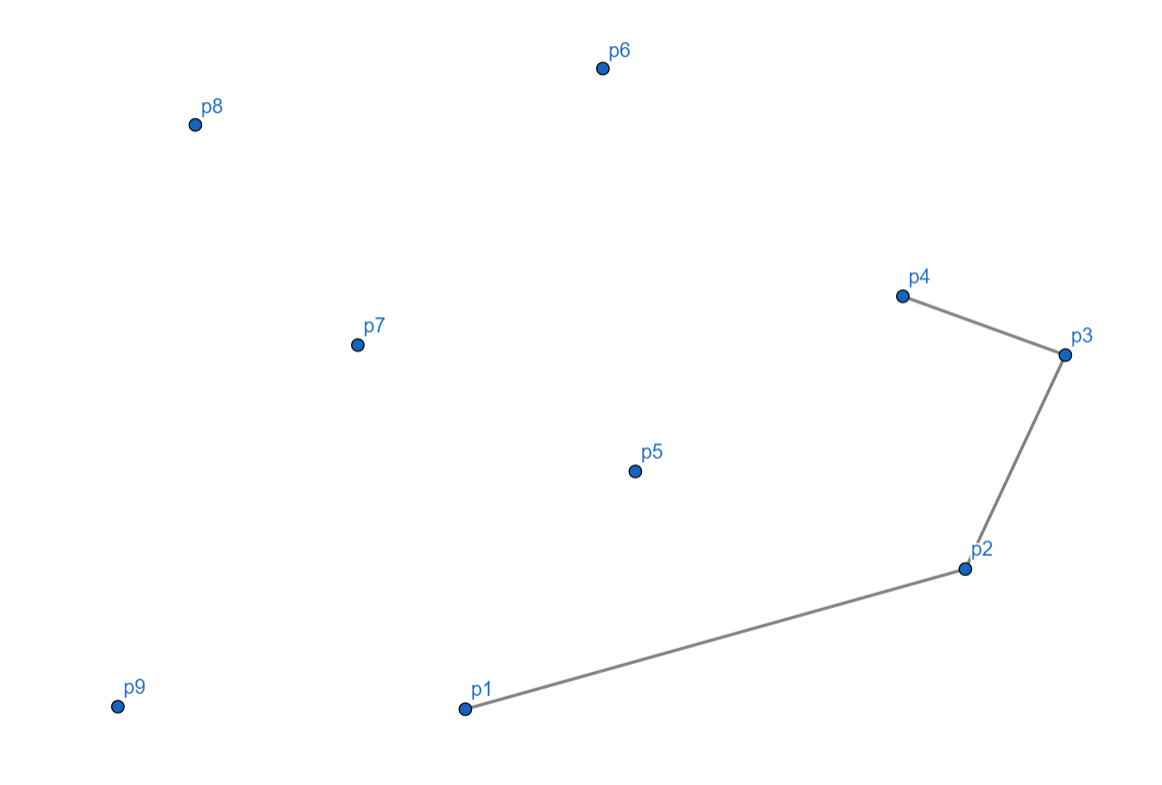
(p_5) 依然向左,入栈。
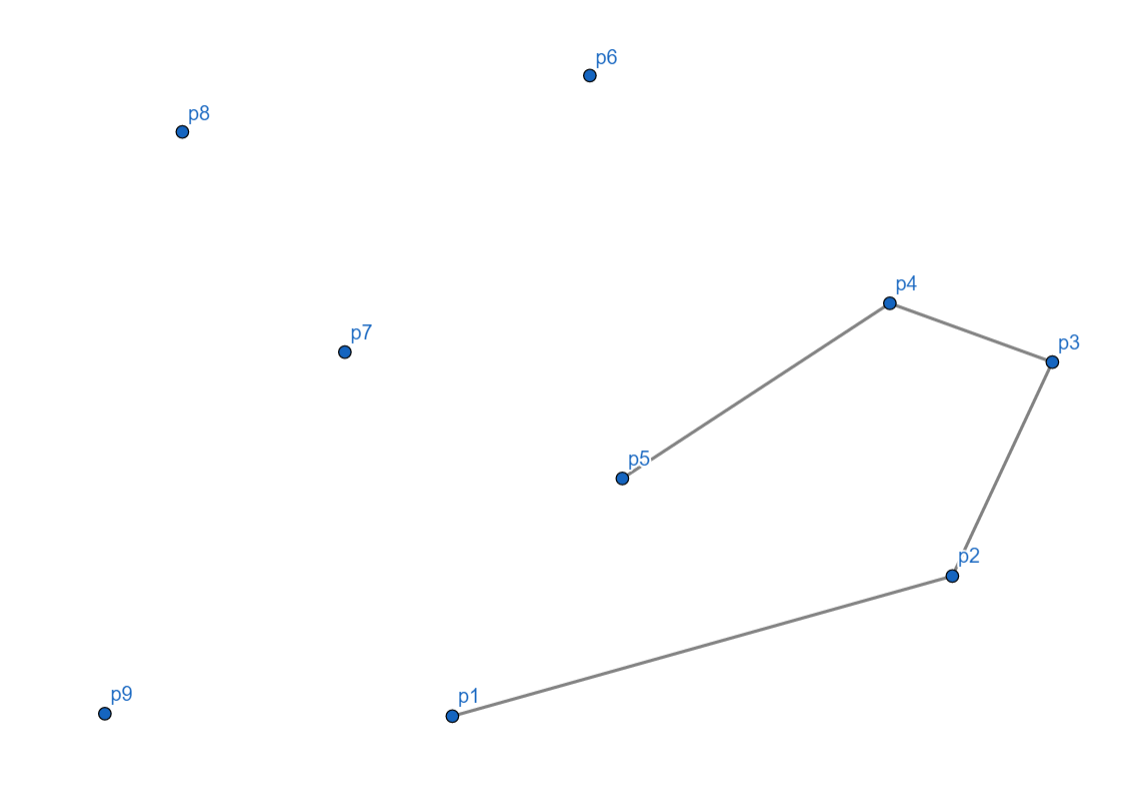
到 (p_6) 时,我们发现了点问题,就是不再是向左了,而是向右了,所以我们此时要将 (p_5) 出栈,(p_6) 入栈。
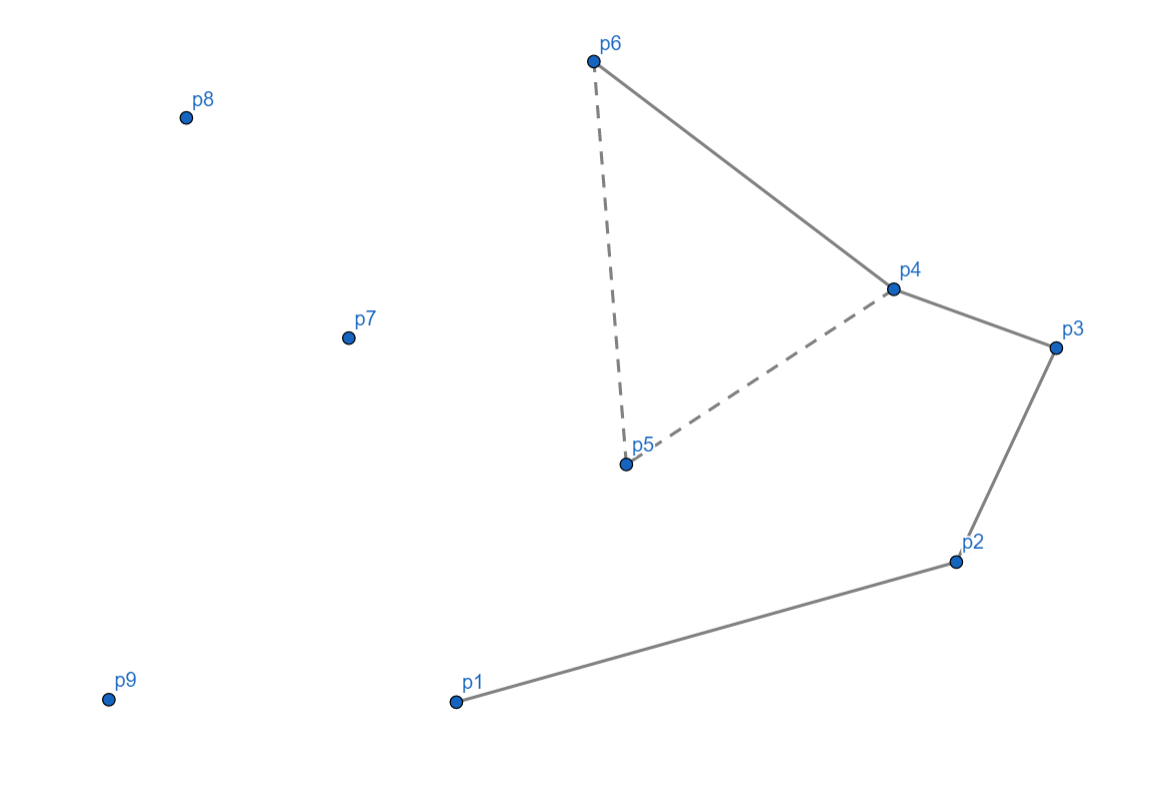
入栈后,我们发现,相对于 (p_4),(p_6) 依然是向右的,所以我们还要把 (p_4) 出栈,(p_6) 入栈。
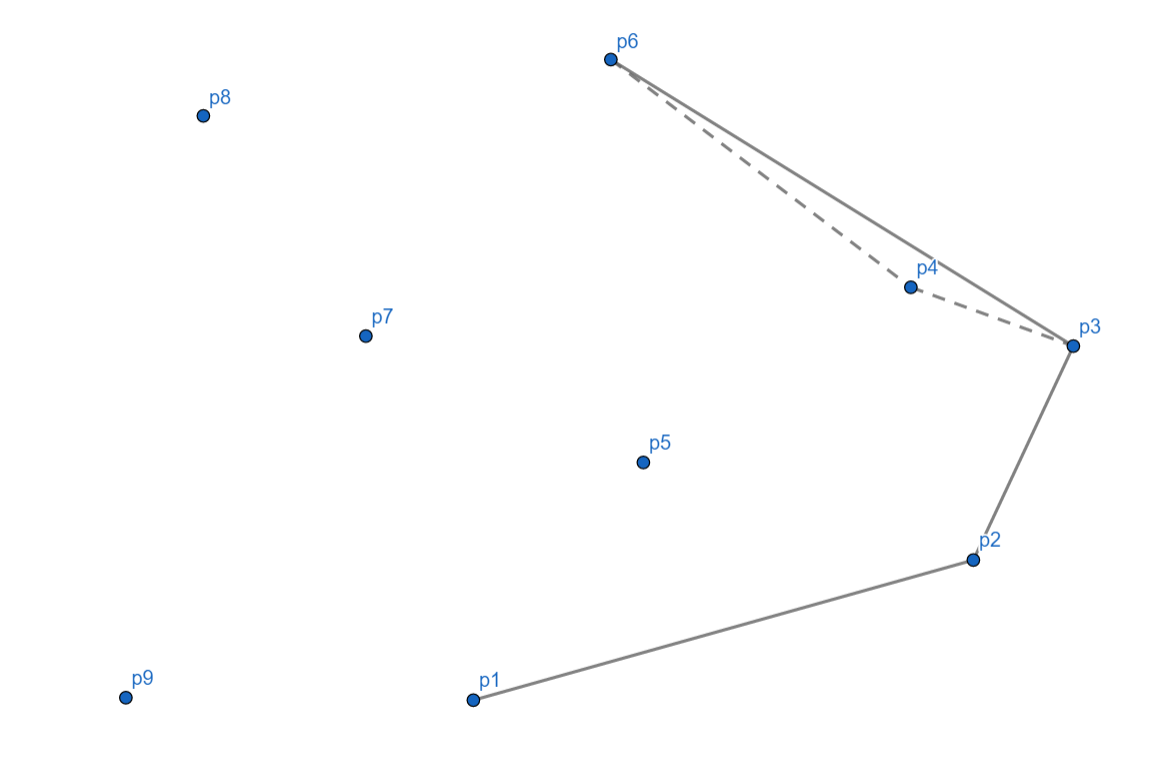
接下来 (p_7) 没有问题。
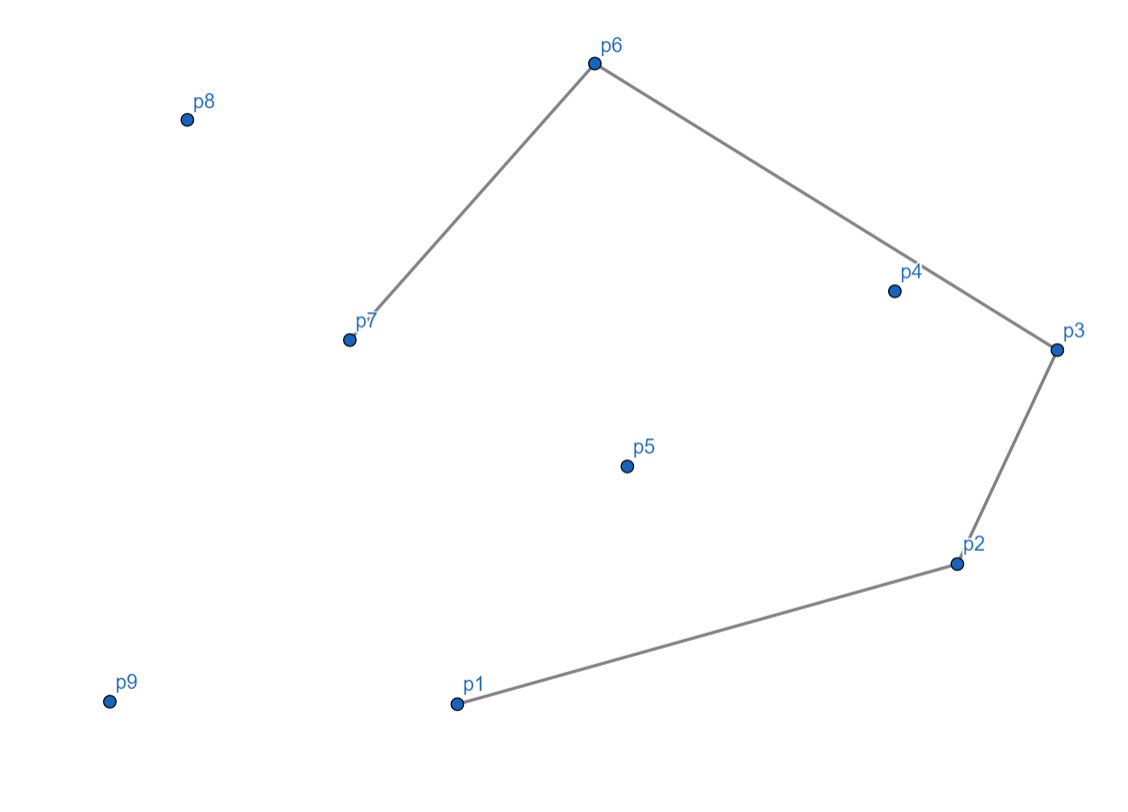
(p_8) 时,我们发现,也是向右的,所以将 (p_7) 出栈,(p_8) 入栈。
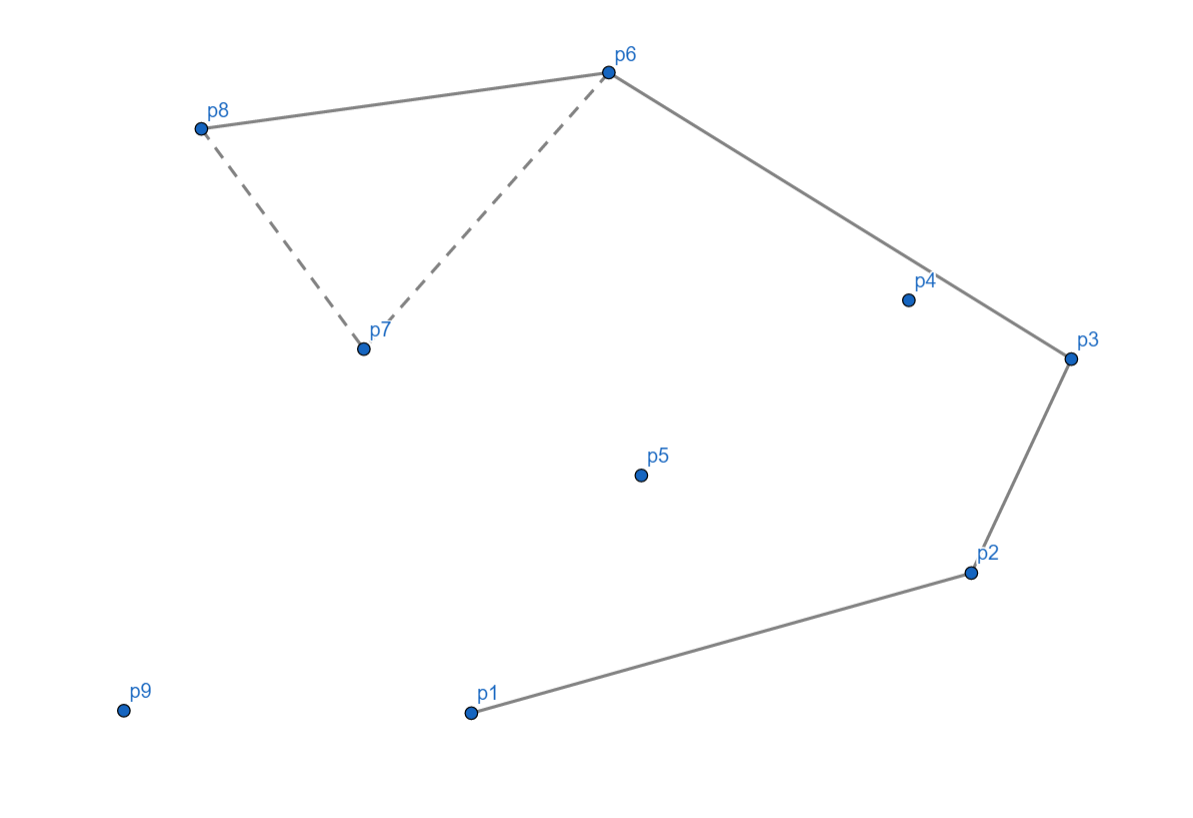
接下来 (p_9) 正常,入栈。
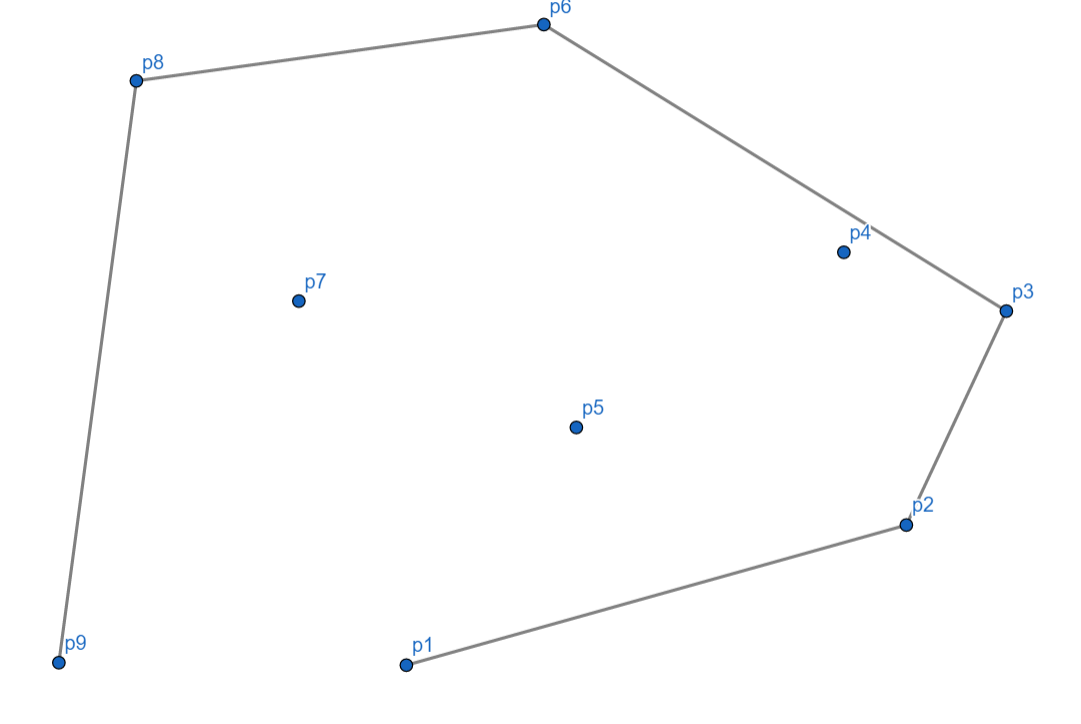
最后,我们再把最后一个点和第一个点连起来。
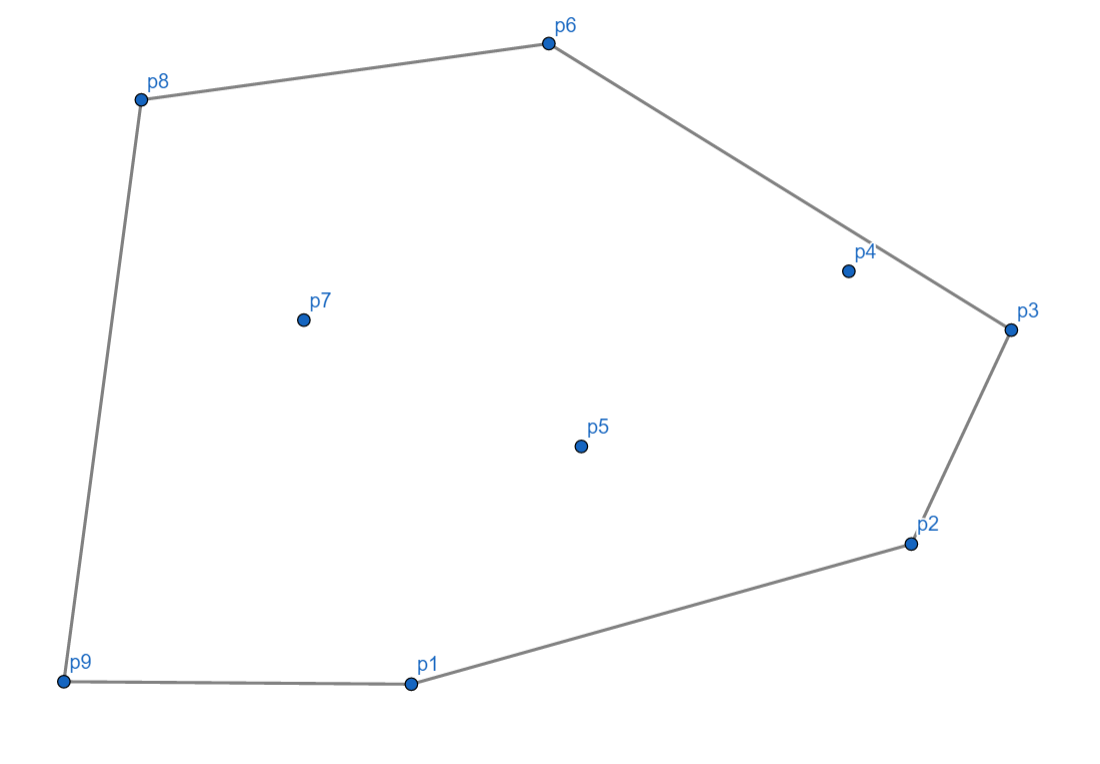
此时,我们的 Graham 算法的全过程就结束了。
扫描的时间复杂度:(O(n))。
但是不可能那么优秀,还要加上排序的时间复杂度:(O(nlog n))。
所以总时间复杂度为 (O(n log n))。
可见此算法相比之前的算法优秀的多。
这道题,我们就用 Graham 算法求凸包。
直接按照 Graham 算法思路一步一步走即可。
Code
/*
Problem:UVA681
Date:02/07/20 14:56
*/
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<cmath>
#include<string>
#define line cout << endl
using namespace std;
const int NR = 1e6 + 5;
int t;
int n;
struct point {
int x, y;
};
point p[NR], ps[NR];
double dis (point pa, point pb) {
return sqrt (1.0 * (pb.x - pa.x) * (pb.x - pa.x) + 1.0 * (pb.y - pa.y) * (pb.y - pa.y));
}
int cp (point pa1, point pa2, point pb1, point pb2) {
return (pa2.x - pa1.x) * (pb2.y - pb1.y) - (pb2.x - pb1.x) * (pa2.y - pa1.y);
}
bool cmp (point px, point py) {
if (px.x == py.x && px.y == py.y) return false;
int num = cp (p[1], px, p[1], py);
if (num > 0) return true;
if (num == 0 && dis (p[0], px) < dis (p[0], py)) return true;
return false;
}
int convex_hull () {
sort (p + 2, p + n + 1, cmp);
ps[1] = p[1];
int h = 1;
for (int i = 2; i <= n; i++) {
while (h > 1 && cp (ps[h - 1], ps[h], ps[h], p[i]) <= 0) {
h--;
}
h++;
ps[h] = p[i];
}
ps[h + 1] = p[1];
return h;
}
void _memset () {
memset (p, 0, sizeof p);
memset (ps, 0, sizeof ps);
return;
}
int main () {
// freopen ("UVA681.in", "r", stdin);
// freopen ("UVA681.out", "w", stdout);
cin >> t;
cout << t << endl;
while (t--) {
cin >> n;
for (int i = 1; i <= n; i++) {
cin >> p[i].x >> p[i].y;
if(i != 1 && p[i].y < p[1].y) {
swap (p[i].y, p[1].y);
swap (p[i].x, p[1].x);
}
}
if (t >= 1) {
int a;
cin >> a;
}
int h = convex_hull ();
cout << h + 1 << endl;
for (int i = 1; i <= h; i++) {
cout << ps[i].x << " " << ps[i].y << endl;
}
cout << ps[1].x << " " << ps[1].y << endl;
if (t >= 1) {
cout << "-1" << endl;
}
_memset ();
}
return 0;
}