大小比较

前言

高中数学中涉及大小比较的数学素材和知识点，大小比较是高中数学中比较常见的一种题型，在不等式、函数、定积分，以及构造函数中，都会见到其影子，现对其进行整理，以便于学习。

理论依据

• 利用作差法或作商法比较大小；比较代数式大小，判断数列的单调性；

• 利用单调性比较大小；

常见类型

• 1、利用不等式性质，对代数式大小比较，

作差法或作商法，常用变形：平方做差法、取对数做差法等

例1【代数式】若(P=sqrt{a+2}+sqrt{a+5})，(Q=sqrt{a+3}+sqrt{a+4}(age 0))，比较(P、Q)的大小。

分析：由于(age 0)，(P > 0)，(Q > 0)，

则有(Q^2-P^2=2a+7+2sqrt{a^2+7a+12}-(2a+7+2sqrt{a^2+7a+10}))

(=2(sqrt{a^2+7a+12}- sqrt{a^2+7a+10}) > 0)，所以(Q^2 > P^2)，则(Q > P)。

例2试比较(16^{18})和(18^{16})的大小关系；

法1：作商法，(cfrac{16^{18}}{18^{16}}=(cfrac{16}{18})^{16}cdot 16^2=(cfrac{8}{9})^{16}cdot 2^8)

(=(cfrac{64}{81})^{8}cdot 2^8=(cfrac{128}{81})^{8}>1)，故(16^{18}>18^{16})；

法2：取对数作差法，(lg16^{18}-lg18^{16}=18lg16-16lg18)

(=72lg2-16(lg2+2lg3)=56lg2-32lg3>0)，故(16^{18}>18^{16})；

• 2、利用具体函数的单调性进行大小比较，常用变形；

涉及函数有二次函数，指数函数，对数函数，幂函数，三角函数，此时大多只涉及一类函数，

例3【幂函数】 幂函数的图像经过点((cfrac{1}{2}，cfrac{sqrt{2}}{2}))，若(0< a < b < 1)，试比较(f(a)、f(b)、f(1)、f(cfrac{1}{a})、f(cfrac{1}{b}))的大小。

分析：设幂函数解析式为(y=x^{alpha})，由 幂函数的图像经过点((cfrac{1}{2}，cfrac{sqrt{2}}{2}))，

则((cfrac{1}{2})^{alpha}=cfrac{sqrt{2}}{2})，即(2^{-alpha}=2^{-frac{1}{2}})，故(alpha=cfrac{1}{2})，故幂函数为(y=x^{frac{1}{2}})，

则其在定义域([0，+infty))上单调递增。又由于(0 < a < b < 1)，则可知(cfrac{1}{a}>cfrac{1}{b}>1)，

即(0 < a < b < 1 <cfrac{1}{b} < cfrac{1}{a})，故有(f(a) < f(b) < f(1) < f(cfrac{1}{b}) < f(cfrac{1}{a}))。

例4【指数函数】设(y_1=4^{0.7})，(y_2=8^{0.45})，(y_3=(cfrac{1}{2})^{-1.5})，比较(y_1，y_2，y_3)的大小。

分析：(y_1=4^{0.7}=2^{1.4})，(y_2=8^{0.45}=2^{1.35})，(y_3=(cfrac{1}{2})^{-1.5}=2^{1.5})，

又(y=2^x)在(R)上单调递增，故(y_2 < y_1 < y_3)；

例5【幂、指数函数】设(a=(cfrac{3}{5})^{frac{2}{5}})，(b=(cfrac{2}{5})^{frac{3}{5}})，(c=(cfrac{2}{5})^{frac{2}{5}})，试比较(a、b、c)的大小。

分析：比较(a、c)，利用幂函数(y=x^{cfrac{2}{5}})，在((0，+infty))上单调递增，故(a > c)；

比较(b、c)，利用指数函数(y=(cfrac{2}{5})^x)，在((-infty，+infty))上单调递减，故(c > b)；

故有(a > c > b)。

例5+1【三角函数】设(a=cfrac{1}{2}cos2^{circ}-cfrac{sqrt{3}}{2}sin2^{circ})，(b=cfrac{2tan14^{circ}}{1-tan^214^{circ}})，(c=sqrt{frac{1-50^{circ}}{2}})，则有【】

$A.a < c < b$ $B.a < b < c$ $C.b < c < a$ $D.c < a < b$

分析：由题目可知，(a=sin(30^{circ}-2^{circ})=sin28^{circ})，(b=tan28^{circ})，(c=sin25^{circ})，则(c<a<b)，故选(D)；

• 3、利用代数式的取值范围进行大小比较，此时涉及多个函数的单调性和值域问题；

涉及函数有二次函数，指数函数，对数函数，幂函数，三角函数，

例6设(a=log_{frac{1}{2}}2)，(b=lnfrac{pi}{2})，(c=2^{frac{1}{pi}})，试比较(a、b、c)的大小。

分析：(a=log_{frac{1}{2}}2 < 0)，(0< b=lnfrac{pi}{2} < 1)，(c=2^{frac{1}{pi}} >1)，

故有(a < b < c)。

例7若(xin (e^{-1}，1))，(a=lnx)，(b=(cfrac{1}{2})^{lnx})，(c=e^{lnx})，则其大小关系为__________。

分析：借助赋值法，令(x=cfrac{1}{2})，则可知(b=(cfrac{1}{2})^{lnx}>1)，(a=lnx<0)，(c=e^{lnx}=cfrac{1}{2})，故大小关系为(b>c>a)；

• 4、利用赋值法比较大小

例7【2019届高三理科数学三轮模拟试题】若(0<a<b<1)，则(a^b)，(b^a)，(log_ba)，(log_ab)的大小关系为【】

$A.a^b > b^a > log_ba > log_{frac{1}{a}} b$ $B.b^a > a^b > log_{frac{1}{a}} b> log_ba $

$C.log_ba > a^b > b^a >log_{frac{1}{a}} b$ $D.log_ba > b^a > a^b >log_{frac{1}{a}} b$

法1：赋值法，令(a=cfrac{1}{4})，(b=cfrac{1}{2})，计算比较得到， (log_ba > b^a > a^b >log_{frac{1}{a}} b)，故选(D).

法2：不等式性质法，由于(0<a<b<1)，则(1>b^a>a^a>a^b>0)，(log_ba>log_bb=1)，

又由于(0<a<1)，则(cfrac{1}{a}>1)，则(log_{frac{1}{a}} b<0)，

综上， (log_ba > b^a > a^b >log_{frac{1}{a}} b)，故选(D).

• 5、利用中间参量进行大小比较；

涉及函数有二次函数，指数函数，对数函数，幂函数，三角函数，此时只是单纯的一类函数，中间参量常常取(0)，(1)等这些简单而特殊的值。

例7大小比较：(log_34)和(log_45)；

法1：由于(log_34=log_3(3 imes cfrac{4}{3})=1+log_3 cfrac{4}{3})，(log_45=log_4(4 imes cfrac{5}{4})=1+log_4cfrac{5}{4})，

因为底数都大于1，所以都是增函数，(cfrac{4}{3}>cfrac{5}{4})，

则(log_3cfrac{4}{3}>log_3cfrac{5}{4})，(log_3cfrac{5}{4}>log_4cfrac{5}{4})，

所以(log_3cfrac{4}{3}>log_4cfrac{5}{4})，即(log_34>log_45)；

法2：取(cfrac{5}{4})为中间量，

(log_34-cfrac{5}{4}=cfrac{lg4}{lg3}-cfrac{5}{4})

(=cfrac{4lg4-5lg3}{4lg3}=cfrac{lgcfrac{4^4}{3^5}}{4lg3}>0)，

即(log_34>cfrac{5}{4})

(log_45-cfrac{5}{4}=cfrac{lg5}{lg4}-cfrac{5}{4})

(=cfrac{4lg5-5lg4}{4lg4}=cfrac{lgcfrac{5^4}{4^5}}{4lg4}<0)，

即(log_45<cfrac{5}{4})，

即(log_34>log_45)；

• 6、利用形进行大小比较；

可能会涉及图形的面积、体积、或长度、角度等，

例8【定积分比较大小】若(s_1=displaystyleint_{1}^{2}x^2;dx)，(s_2=displaystyleint_{1}^{2}cfrac{1}{x};dx)，(s_3=displaystyleint_{1}^{2}e^x;dx)，则(S_1，S_2，S_3)的大小关系如何？

法1：从数的角度，计算定积分的大小，从而比较大小，过程略。(S_2 < S_1 < S_3)。

法2：从形的角度，利用定积分的几何意义，借助图形的面积直观比较大小。(S_2 < S_1 < S_3)。

高阶拔高

• 7、构造函数进行大小比较；

涉及构造函数，大难点，抽象函数的具体函数，

例10【2017•渭南模拟】已知定义域为R的奇函数(y=f(x))的导函数为(y=f'(x))，当(x> 0)时，(f'(x)+cfrac{f(x)}{x}>0)，若(a=cfrac{1}{3}f(cfrac{1}{3})，b=-3f(-3)，c=(lncfrac{1}{3})f(lncfrac{1}{3}))，则(a，b，c)的大小关系正确的是　 【 】

$A.a < b < c$ $B.a < c < b$ $C.b < c < a$ $D.c < a < b$

分析：当(x> 0)时，(f'(x)+cfrac{f(x)}{x}>0)，即(xf'(x)+f(x)>0)，

故构造函数(g(x)=xcdot f(x))，由于(y=f(x))与(y=x)都是奇函数，则函数(g(x))为偶函数，

当(x >0)时，(g'(x)=f(x)+xf'(x) >0)，即函数(g(x))在([0，+infty))上单调递增，

由偶函数可知，函数(g(x))在((-infty，0])上单调递减。

而(a=cfrac{1}{3}f(cfrac{1}{3})=g(cfrac{1}{3}))，

(b=-3f(-3)=g(-3)=g(3))，

(c=(lncfrac{1}{3})f(lncfrac{1}{3})=g(lncfrac{1}{3})=g(-ln3)=g(ln3))，

又(cfrac{1}{3} < ln3 < 3)，故(g(cfrac{1}{3}) < g(ln3) < g(3))，即(a < c < b)，故选B.

例11【构造函数+大小比较】【2017(cdot)河南平顶山一模】已知(f(x))是定义在((0，+infty))上的函数，对任意两个不相等的正数(x_1，x_2)，都有(cfrac{x_2f(x_1)-x_1f(x_2)}{x_1-x_2}>0)，记(a=cfrac{f(3^{0.2})}{3^{0.2}})，(b=cfrac{f(0.3^2)}{0.3^2})，(c=cfrac{f(log_25)}{log_25})，则【】

$A.a < b < c$ $B.b < a < c$ $C.c < a < b$ $D.c < b < a$

分析：注意到(a，b，c)的结构，由题目猜想：要构造的函数是(g(x)=cfrac{f(x)}{x})，

那么是否正确，以下做以验证。

令(0< x_1< x_2)，则由单调性定义的等价形式可得，

(cfrac{g(x_1)-g(x_2)}{x_1-x_2}=cfrac{cfrac{f(x_1)}{x_1}-cfrac{f(x_2)}{x_2}}{x_1-x_2}=cfrac{x_2f(x_1)-x_1f(x_2)}{x_1x_2(x_1-x_2)})

由题目，对任意两个不相等的正数(x_1，x_2)，都有(cfrac{x_2f(x_1)-x_1f(x_2)}{x_1-x_2} >0)，

则可知(cfrac{g(x_1)-g(x_2)}{x_1-x_2} >0)，即函数(g(x)=cfrac{f(x)}{x})是单调递增的，

故题目需要我们比较(g(3^{0.2}))，(g(0.3^2))，(g(log_25))这三个的大小关系，

只需要比较自变量的大小就可以了；

由于(1=3^0 < 3^{0.2} < 3^{0.5}=sqrt{3} <2)，(0 < 0.3^2=0.09 <1)，(log_25 > log_24=2)，

故(g(0.3^2) < g(3^{0.2}) < g(log_25))，即(b < a < c)。故选(B).

需要记忆

下述结论中的结论2和结论3，在函数与导数的高阶考察中常常会作为变形的基础，故需要认真理解记忆。

结论1【三角函数比较大小】三角函数章节中的重要不等式：( hetain (0，cfrac{pi}{2}))时，(sin heta < heta < tan heta)。

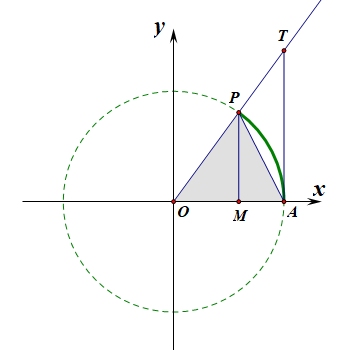
【证法1】：三角函数线法，如图所示为单位圆，则(sin heta=MP)，(tan heta=AT)，(overset{frown}{AP}= hetacdot 1= heta)

由图可知，(S_{Delta OAP} < S_{扇形 OAP} < S_{Delta OAT})

即(cfrac{1}{2}cdot |OA|cdot MP < cfrac{1}{2}cdot heta cdot |OA| <cfrac{1}{2}cdot |OA|cdot AT)

则有(MP < heta < AT)，即(sin heta < heta < tan heta)。

故( hetain (0，cfrac{pi}{2}))时，(sin heta < heta < tan heta)。

【证法2】：构造函数法，如令(g(x)=sinx-x)，(xin (0，cfrac{pi}{2}))，

则(g'(x)=cosx-1leq 0)恒成立，故(g(x))在(xin (0，cfrac{pi}{2}))上单调递减，

故(g(x) < g(0)=0)，即(sinx < x)，同理可证(x < tanx)，

故( hetain (0，cfrac{pi}{2}))时，(sin heta < heta < tan heta)。

结论2(e^x>x+1(x eq 0))

证明思路：【法1】数形结合法，令(f(x)=e^x)，(g(x)=x+1)，在同一个坐标系中作出这两个函数的图像，

由图像可知，当(x eq 0)时，都满足关系(e^x>x+1)。

补充：至于函数(f(x)=e^x)和函数(g(x)=x+1)为什么会相切与点((0，1))，

我们可以用导数方法来解答。

【法2】作差构造函数法，令(h(x)=e^x-x-1)，则(h'(x)=e^x-1) ，

当(x<0)时，(h'(x)<0)；当(x>0)时，(h'(x)>0)；

即函数(h(x))在((-infty，0))上单调递减，在((0，+infty))上单调递增，

故函数(h(x)_{min}=h(0)=0)，故(h(x)ge 0)，当且仅当(x=0)时取到等号，

故(x eq 0)时，总有(h(x)>0)，即(e^x>x+1)。

结论3(lnxleq x-1(x>0))

证明思路：【法1】数形结合法，令(f(x)=lnx)，(g(x)=x-1)，

在同一个坐标系中作出这两个函数的图像，

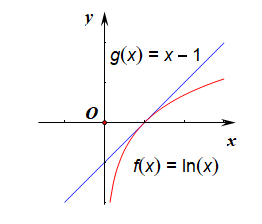
由图像可知，当(x> 0)时，都满足关系(lnxleq x-1)。

【法2】：作差构造函数法，令(h(x)=lnx-x+1(x>0))，则(h'(x)=cfrac{1}{x}-1)，

当(0<x<1)时，(h'(x)>0)；当(x>1)时，(h'(x)<0)；

即函数(h(x))在((0，1))上单调递增，在((1，+infty))上单调递减，

故函数(h(x)_{max}=h(1)=0)，故(h(x)leq 0)，当且仅当(x=1)时取到等号，

故(x> 0)时，总有(h(x)leq 0)，即(lnxleq >x-1)。

【法3】利用反函数法，此法主要基于(e^xge x+1)的结论，

由于函数(y=e^x)以及函数(y=x+1)关于直线(y=x)的对称函数

分别是(y=lnx)和函数(y=x-1)，故得到(lnxleq x-1)。

【法4】：利用代数变换，由(e^xge x+1)，两边取自然对数得到(lne^xge ln(x+1))，

即(xge ln(x+1))，再用(x-1)替换(x)，得到(x-1ge lnx)，即(lnxleq x-1)。

典例剖析

例9【2017全国卷1理科第11题】已知(2^x=3^y=5^z)，比较(2x、3y、5z)的大小；

分析：令(2^x=3^y=5^z=k)，则(x=log_2k=cfrac{lgk}{lg2})，(y=log_3k=cfrac{lgk}{lg3})，(z=log_5k=cfrac{lgk}{lg5})，

故(2x=cfrac{2lgk}{lg2}=cfrac{lgk}{cfrac{1}{2}lg2}=cfrac{lgk}{lgsqrt{2}})，

(3y=cfrac{3lgk}{lg3}=cfrac{lgk}{cfrac{1}{3}lg3}=cfrac{lgk}{lgsqrt[3]{3}})，

(5z=cfrac{5lgk}{lg5}=cfrac{lgk}{cfrac{1}{5}lg5}=cfrac{lgk}{lgsqrt[5]{5}})，接下来，

法1：(单调性法)转化为只需要比较(sqrt[2]{2})，(sqrt[3]{3})，(sqrt[5]{5})三者的大小即可。

先比较(sqrt[2]{2})，(sqrt[3]{3})，给两个式子同时6次方，

得到((sqrt[2]{2})^6=2^3=8)，((sqrt[3]{3})^6=3^2=9)，

故(sqrt[2]{2}<sqrt[3]{3})，则(cfrac{lgk}{lgsqrt[2]{2}}>cfrac{lgk}{lgsqrt[3]{3}})，

即得到(2x>3y)

再比较(sqrt[2]{2})，(sqrt[5]{5})，给两个式子同时10次方，

得到((sqrt[2]{2})^{10}=2^5=32)，((sqrt[5]{5})^{10}=5^2=25)，

故(sqrt[2]{2}>sqrt[5]{5})，则(cfrac{lgk}{lgsqrt[2]{2}}<cfrac{lgk}{lgsqrt[3]{3}})，

即得到(5z>2x)，综上得到(3y<2x<5z)

法2：(作差法)

(2x-3y=cfrac{2lgt}{lg2}-cfrac{3lgt}{lg3}=cfrac{lgt(2lg3-3lg3)}{lg2lg3}=cfrac{lgt(lg9-lg8)}{lg2lg3}>0)，

故(2x>3y);

(2x-5z=cfrac{2lgt}{lg2}-cfrac{5lgt}{lg5}=cfrac{lgt(2lg5-5lg2)}{lg2lg5}=cfrac{lgt(lg25-lg32)}{lg2lg5}<0)

故(2x<5z);

综上有(3y<2x<5z)。

法3：(作商法)

(cfrac{2x}{3y}=cfrac{2}{3}cdot cfrac{lg3}{lg2}=cfrac{lg9}{lg8}=log_89>1)，故(2x>3y)；

(cfrac{5z}{2x}=cfrac{5}{2}cdot cfrac{lg2}{lg5}=cfrac{lg2^5}{lg5^2}=log_{25}32>1)，

故(5z>2x)；故(3y<2x<5z)。素材链接