**I,水管局长数据加强版 **
题目描述 : 给定一张图,每次询问两点之间的最短路,有删边
其实是(LCT)动态维护最小生成树的板子题来着
由于蒟蒻并不会下放边权之类的神奇操作,所以来一波边化点
由于有删边而没有加边,我们把时间倒序就可以变成有删边没有加边了
**II,GERALD07加强版 **
题目描述 : 给定一些边,询问区间([l,r])的联通块个数,强制在线
我们知道对于森林来说,联通块数=点数-边数
那么我们把题意转化成了询问区间([l,r])的边做生成树后的边数
考虑预处理
我们可以依次扫每条边,尝试把他们加入LCT
如果边的两端不在同一棵树中显然可以直接(link)
现在考虑在同一棵树中
这时这条边和树上的边构成了一个简单环
那么我们是不是直接断掉环上一条边就好了呢
断哪条?显然是环上最早加入的那一条啊,这个LCT维护一下就行了
于是我们得到了如下算法:
每次尝试加入一条边
若合法,直接加入并在主席树对应的位置插入
否则,找到环上时间最早的边断掉并在主席树中相应位置减去,在加入当前边
每次询问主席树上(R)的树中([L,R])这个区间就行了
III,魔法森林
题目描述 : 给定一张图,每条边有两个边权,求(1)到(n)的路径中(max(A_i)+max(B_i))的最小值
其实和第一题差不多啊
先按照(A)排序,依次把边加入
若产生了环,把环上B最大的边删去就行了
IV,情报传递
题目描述 : 询问树上((u,v))路径中小于等于某个值的数个数
这是真的挺裸的了
由于点权随着时间变化增加并不好维护,我们考虑对询问下手
我们发现这个c其实没有什么意义,直接把这个询问放到(i-c-1)的位置上就行了
然后就没了
V,LCA
题目描述 : 给定一棵树,每次询问(l,r,z),输出(sumlimits_{i=l}^{r}dep[lca(i,z)])
在线不好做,考虑离线
我们知道一个点和其他点的(lca)一定在他到根的路径上(废话)
那么问题转化成了询问区间([l,r])中的点往根走,最早遇到的(z)到根上路径中点的深度之和
然后我们给深度转化一下含义,(dep_{i})为(i)到根路径上的点的个数
然后看一下lca的深度的含义
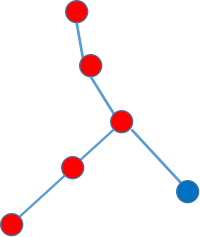
假如我们从某个点向上标记到根(如图)
然后查询另一个点时,我们发现他们lca作出的贡献就是另一个点在他到根路径上的标记数
所以我们按照点的编号一个一个标记他们根路径上的点,在每个询问的(l-1)和(r)处分别做一次查询
最后输出(ans_r-ans_l)就行了
VI,在美妙的数学王国中畅游
题目描述 : 一棵树,树点上各有一个函数,求对于一条路径(u,v)和初值x,sumlimits_{tin (u,v)}f_t(x)
%%%LNC
VII,即使战略(交互题)
题目描述 : 有一棵树,初始只有(1)号节点探索过,每次可以调用(explore(x,y)),返回路径((x,y))上第二个点,要求在规定次数内探索完整棵树
链的情况其实不是很难
我们维护当前区间的左右端点,每次从一个端点开始探索,若得到已走过的点说明目前的目标点在区间的另一边,直接从另一端怼过去就好了
否则直接从这一端怼过去
然后考虑树的情况
有一个很暴力的思路:每次直接从根走到目标点,这显然是不对的(指复杂度)
直接从根跳到叶子复杂度不对,但是有什么方法可以快速跳到叶子呢
我们考虑在(splay)上二分
每次调用&explore&找到已知点会有三种情况
- 1,前趋
- 2,后继
- 3,在另一棵(splay)上
对于前两种,直接走到当前点的左/右儿子
对于第三种,直接跳到那棵(splay)的根
这样期望探索次数是(nlog)的(虽然窝不会证)
记得把要探索的点(random)_(shuffle)一下
VIII,大森林
题目描述 : 小 Y 家里有一个大森林,里面有 棵树,编号从 到 。一开始这些树都只是树苗,只有一个节点,标号为 。这些树都有一个特殊的节点,我们称之为生长节点,这些节点有生长出子节点的能力。小 Y 掌握了一种魔法,能让第 棵树到第 棵树的生长节点长出一个子节点。同时她还能修改第 棵树到第 棵树的生长节点。她告诉了你她使用魔法的记录,你能不能管理她家的森林,并且回答她的询问呢?
大神题啊。。。。。。
这种怎么看都不能直接做的题多半是要离线了
我们发现0操作对询问没有影响,也就是说可以先让所有点长出来再回答询问
而对于1操作,我们可以用到一个虚点的套路
对于每个1操作建一个虚点,以后的0操作都连在最近建好的虚点上
这样1操作就被拆成了两次断边连边
综上,
我们先把所有的虚点用LCT相连
扫所有操作,遇到断边连边就用LCT来嫁接
对于所有查询......
等等,这玩意怎么查询
因为我们建了虚点,导致split之后不能保证路径上所有点都在splay里,答案就不对了啊
那么就来一波树上差分吧用(len(x,y)=dep_x+dep_y-2 imes dep_{lca})
什么你说(LCT)怎么求(LCA)?(把T换成A)
先(access(x))并(splay(x)),这时形成了一个以根到(x)的路径上的点构成的(splay)
然后(access(y))最后到达(x)所在(splay)时的那个点就是(lca)啦