PCA(主成分分析)方法浅析
降维、数据压缩
找到数据中最重要的方向:方差最大的方向,也就是样本间差距最显著的方向
PCA算法主要用于降维,就是将样本数据从高维空间投影到低维空间中,并尽可能的在低维空间中表示原始数据。PCA的几何意义可简单解释为:
0维-PCA:将所有样本信息都投影到一个点,因此无法反应样本之间的差异;要想用一个点来尽可能的表示所有样本数据,则这个点必定是样本的均值。
1维-PCA:相当于将所有样本信息向样本均值的直线投影;
2维-PCA:将样本的平面分布看作椭圆形分布,求出椭圆形的长短轴方向,然后将样本信息投影到这两条长短轴方向上,就是二维PCA。(投影方向就是平面上椭圆的长短轴方向);
3维-PCA:样本的平面分布看作椭圆形分布,投影方法分别是椭圆球的赤道半径a和b,以及是极半径c(沿着z轴);
PCA简而言之就是根据输入数据的分布给输入数据重新找到更能描述这组数据的正交的坐标轴,比如下面一幅图,对于那个椭圆状的分布,最方便表示这个分布的坐标轴肯定是椭圆的长轴短轴而不是原来的x ,y轴。
那么如何求出这个长轴和短轴呢?于是线性代数就来了:我们需要先求出这堆样本数据的协方差矩阵,然后再求出这个协方差矩阵的特征值和特征向量,对应最大特征值的那个特征向量的方向就是长轴(也就是主元)的方向,次大特征值的就是第二主元的方向,以此类推。
原文链接:https://blog.csdn.net/guyuealian/article/details/68487833
在与第一个正交的超平面上找最合适的第二个方向
PCA算法流程
来源:https://zhuanlan.zhihu.com/p/37777074
输入:数据集
,需要降到k维。
去平均值(即去中心化),即每一位特征减去各自的平均值。
计算协方差矩阵
,注:这里除或不除样本数量n或n-1,其实对求出的特征向量没有影响。
用特征值分解方法求协方差矩阵
的特征值与特征向量。
对特征值从大到小排序,选择其中最大的k个。然后将其对应的k个特征向量分别作为行向量组成特征向量矩阵P。
将数据转换到k个特征向量构建的新空间中,即Y=PX。
这个降维的过程就体现在了选取k这个过程中,选择的k就是降维之后的维度数
PCA原理分析
这篇文章分析的不错:http://jermmy.xyz/2017/12/14/2017-12-15-PCA-another-view/,大家自取吧。我放一点结论出来:
这个新的协方差矩阵有一个很重要的性质,除了对角线上的元素,其他元素通通是 0。要知道,协方差矩阵中,对角线上的元素表示方差,非对角线上的元素表示协方差。这说明,经过 PCA 处理后,我们把原本的数据 *xx,转变成各个分量之间没有任何关系(协方差为 0)的数据 y!我认为这正是 PCA 的精髓所在,也是我们使用 PCA 算法的根本目标。
要知道,这些特征值(或者说方差)都是按照从大到小排序的,也就是说,我们在降维时,舍弃掉了那些特征值比较小的分量。这么做是符合常理的,因为数据的方差越大,证明分布越广,这样,我们还原这些数据的难度是越大的,而方差越小,证明数据分布越集中,还原它们的难度就越小(方差为 0 的话,用一个数就可以代表所有样本了)。所以,降维时,我们尽量保留那些方差大的数据,而忽略那些方差小的。本文开篇的图中给出一个形象的解释,我们把一个二维的数据映射到一维时,也是优先映射到方差大的那一维上,这样,原数据的分布规律可以最大限度的保留下来,信息的保留也是最完整的。
主成分选择
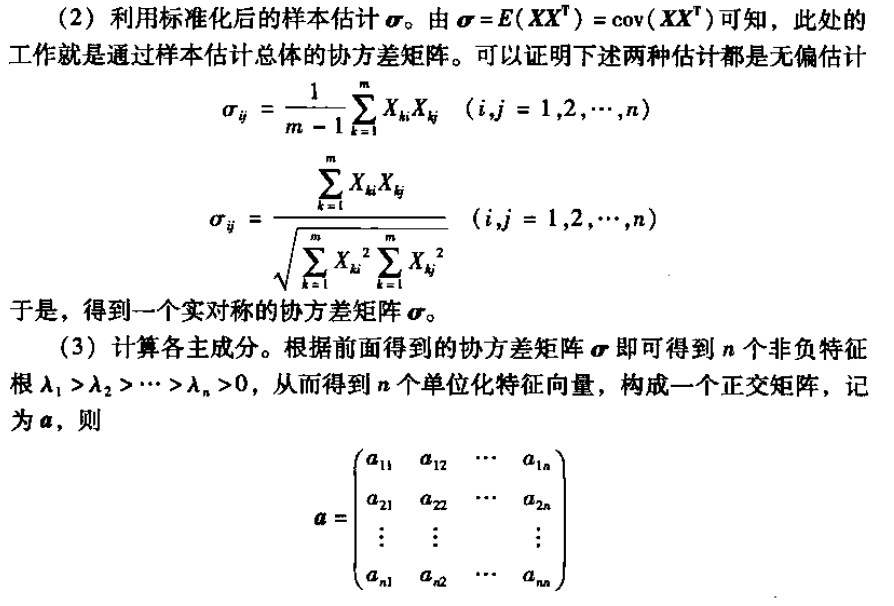
以下内容来自于《系统工程》课本,是上课的时候无意中发现原来这本书里也有提到PCA,而且写得还不错


另附书上一个计算的例子: