线性代数名词概念梳理
线性代数常常见的P矩阵(Permutation)(交换矩阵又叫做置换矩阵)。P矩阵是单位矩阵交换行所成,所以P的每列都是正交,所以它是正交矩阵,所以。当高斯消元法主元有0时候就需要交换行。所以正常是A=LU,但是主元有0时候,那就是PA=LU。
向量空间:一系列向量的集合。在这个集合内任意两个向量通过加减,乘上一个数,线性组合等操作不会出这个空间。比如一条直线它就是一个向量空间。几个向量的线性组合就是一个向量空间。
子空间:包括原点的向量空间是子空间
列空间:就是把矩阵的列拿出来,进行线性组合就得到列空间。
子空间交集一定是子空间,因为要么是相交于原点,要么是在某个子空间内
线性相关:去掉某列仍然能表示某个空间,那就是线性相关。换句话说就是其他列能组合表示它
null space零空间:Ax=0的所有x解集
矩阵空间:就是把矩阵作为单独的一维,就像向量空间一样(向量空间是把向量作为一维)。对矩阵进行线性组合的空间。
LU分解与QR分解
LU分解是想把矩阵A分解成一个下三角矩阵×上三角矩阵,即A=L×U,其中L是Lower Tiangular Matrix的意思U是Upper Triangular Matrix。而QR分解是想把矩阵A分解成一个正交矩阵×上三角矩阵。其中Q代表正交矩阵,R代表右上角Right非零。
LU分解在这篇文章已经介绍了。
从我的理解讲QR分解
网上的基本是用Gram-Schmidt正交按步骤介绍,并没有讲出为何这么做。本文不会按照先执行A操作再执行B操作这种模式介绍,因为这样根本没有任何理解的成分,很容易会忘。
接下来介绍下2×2的QR分解:
2维的QR分解就是把矩阵A
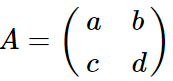
分解成下面这种形式:
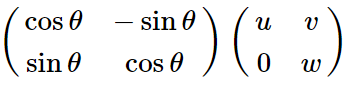
也就是说:
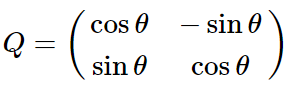
所以把这个式子
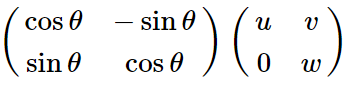
用矩阵乘法乘在一起得到:
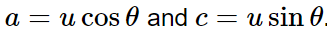
然后上面那个式子两边平方再两个式子相加,并且根据
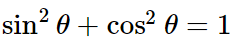
可以得到:
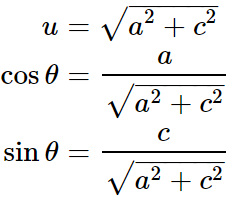
所以现在我们已经求得Q矩阵。并且知道了R矩阵的左上元素。还是根据原先的矩阵乘法有:
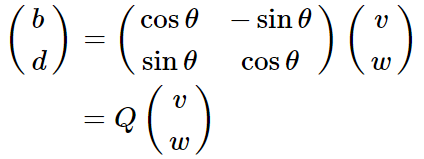
注意了:
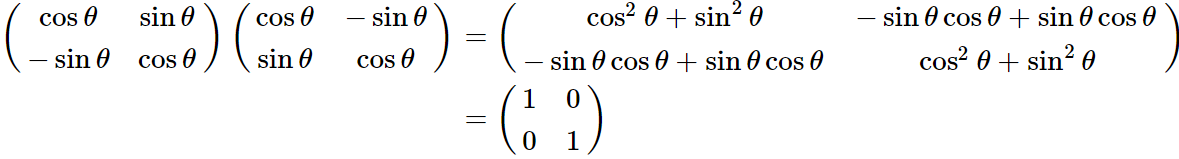
也就是说
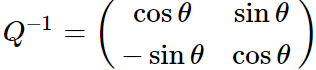
然后我们两边乘个得到:
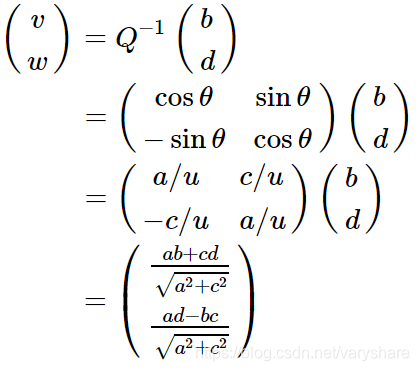
于是我们把R矩阵算出来了。好了QR分解讲完了。
SVD在机器学习,生物,图像处理等领域非常有用。今天就简单介绍后面再详细介绍下SVD分解。
SVD奇异值分解
SVD分解它就是想把矩阵A分解成旋转矩阵×对角矩阵×旋转矩阵这种形式,即下面这种:
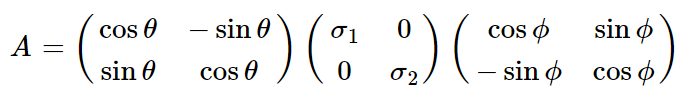
基:n维向量任意n个不线性相关的向量(即两两不平行)就可以组成基。如果这些向量两两正交那就是正交基。为啥叫做基。因为任意n个不线性相关的向量可以表示其他任意向量,所以他们是创始者,基就是创始者的意思。
线性代数一个很大用处就是存储一个图的信息。下面这个叫做图,它可以描述人际关系,可以描述各个地点的远近,可以描述电路的通达。等等。通过矩阵表示他们,可以我们对物理的一些电流计算就会变得简单。
