- 行列式是一个数字。
- 行列式能尽可能的把矩阵的信息表示出来。比如行列式为0矩阵不可逆。
- 交换行或者列行列式变符号,这意味着交换矩阵它的行列式是1或者-1.因为交换矩阵可以把其他矩阵的行列交换。
- 行或者列乘个t,那么整个行列式的值需要乘个t。
- 行列式每行都有可加性
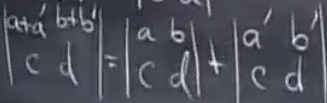
- ,其中是伴随矩阵(当前元素是即去掉当前行当前列的矩阵行列式值)
- 行列式值等于当前行的各元素与对应代数余子式的线性加权和。
克拉默法则(Cramer’s Rule)求Ax=b中的x就是利用伴随矩阵求,然后
行列式的绝对值是行向量那几条边构成的几何体的体积(如果是二维那就是面积)。
特征值
- 特征值之和等于对角线元素之和
- 求特征值
- 越部队称的矩阵特征值越可能是复数
- 特征值不同特征向量一定不线性相关,但是特征值相同不一定特征向量线性相关。
根据特征值和特征向量构造对角矩阵
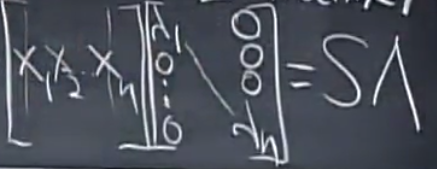
- 矩阵对角化,本质就是利用Ax=λx这个来构造对角矩阵。它构造的对角矩阵的等式为为AS=SΛ.其中Λ是对角矩阵(对角线是特征值),S是特征向量构成的矩阵。如果S可逆(即各个特征向量都不线性相关)那么有:。我们也可以得到一种新的矩阵分解方式:,这种分解的用处是可以求矩阵的幂因为.
左边为(其中x为特征向量):

右边为:
马尔科夫矩阵
矩阵稳定性就是看矩阵的幂是否趋于0,也就是说特征值都的绝对值是不大于1的。或者证明
满足两条性质
- 所有元素大于0
- 每列各元素和等于1.
- 有一个特征值是1
傅里叶级数
,它本质可以视作无穷个正交向量的线性组合。傅里叶级数它要确定这些系数的值。
注意:两个函数的内积
那怎么确定系数值呢?比如我要求那么我两边点乘个cosx,这样就右边只剩下cosx这个项,其他项都是0(因为其他都是相互正交所以是0)。我们用公式表示下这个是什么意思: