这篇博客整理K均值聚类的内容,包括:
1、K均值聚类的原理;
2、初始类中心的选择和类别数K的确定;
3、K均值聚类和EM算法、高斯混合模型的关系。
一、K均值聚类的原理
K均值聚类(K-means)是一种基于中心的聚类算法,通过迭代,将样本分到K个类中,使得每个样本与其所属类的中心或均值的距离之和最小。
1、定义损失函数
假设我们有一个数据集{x1, x2,..., xN},每个样本的特征维度是m维,我们的目标是将数据集划分为K个类别。假定K的值已经给定,那么第k个类别的中心定义为μk,k=1,2,..., K,μk是一个m维的特征向量。我们需要找到每个样本所属的类别,以及一组向量{μk},使得每个样本与它所属的类别的中心μk的距离平方和最小。
首先,这个距离是什么距离呢?聚类需要根据样本之间的相似度,对样本集合进行划分,将相似度较高的样本归为一类。度量样本之间相似度的方法包括计算样本之间的欧氏距离、马氏距离、余弦距离或相关系数,而K均值聚类是用欧氏距离的平方来度量样本之间的相似度。欧式距离的平方公式如下:

把所有样本与所属类的中心之间距离的平方之和定义为损失函数:
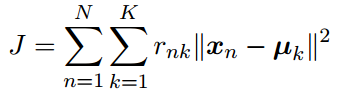
其中rnk∈{0,1},n=1,2,...,N,k=1,2,...,K,如果rnk=1,那么表示样本xn属于第k类,且对于j≠k,有rnj=0,也就是样本xn只能属于一个类别。
于是我们需要找到{rnk}和{μk}的值,使得距离平方之和J最小化。
2、进行迭代
K均值聚类的算法是一种迭代算法,每次迭代涉及到两个连续的步骤,分别对应rnk的最优化和μk的最优化,也对应着EM算法的E步(求期望)和M步(求极大)两步。
首先,为μk选择一些初始值,也就是选择K个类中心。然后第一步:保持μk固定,选择rnk来最小化J,也就是把样本指派到与其最近的中心所属的类中,得到一个聚类结果;第二步:保持rnk固定,计算μk来最小化J,也就是更新每个类别的中心。不断重复这两个步骤直到收敛。
具体来说:
E步:在类中心μk已经确定的情况下,最优化rnk
这一步比较简单,我们可以对每个样本xn独立地进行最优化。将某个样本分配到第k个类别,如果这个样本和第k个类别的距离最小,那么令rnk=1。对N个样本都这样进行分配,自然就得到了使所有样本与类中心的距离平方和最小的{rnk},从而得到了一个聚类结果。
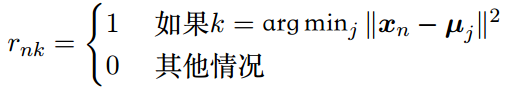
M步:确定了数据集的一种划分,也就是{rnk}确定后,最优化μk
目标函数J是μk的一个二次函数,令它关于μk的导数为零,就可以使目标函数达到最小值,即
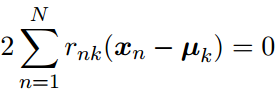
解出μk的结果为:
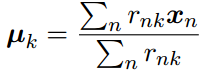
这个μk就是类别k中所有样本的均值,所以把这个算法称为K均值聚类。
重新为样本分配类别,再重新计算每个类别的均值,不断重复这两个步骤,直到聚类的结果不再改变。
需要注意以下几点:
①K均值聚类算法可能收敛到目标函数J的局部极小值,不能保证收敛到全局最小值;
②在聚类之前,需要对数据集进行标准化,使得每个样本的均值为0,标准差为1;
③初始类中心的选择会直接影响聚类结果,选择不同的初始类中心,可能会得到不同的聚类结果。
④K均值聚类算法的复杂度是O(mnk),m是样本的特征维度,n是样本个数,k是类别个数。
二、初始类中心的选择和类别数K的确定
K均值聚类算法的思想比较简单,不涉及到什么数学知识,关键点在于初始类中心的选择和类别数K的确定,这对聚类的结果有比较大的影响。
(一)初始类中心的选择
1、第一种方法
用层次聚类算法进行初始聚类,然后用这些类别的中心作为K均值聚类的初始类中心。层次聚类的复杂度为O(mn3),m是样本的特征维度,n是样本个数,复杂度也是蛮高的,那为什么用层次聚类的结果作为初始类呢?我想是因为层次聚类的结果完全是由算法确定的,完全没有人工的干预,是一个客观的结果,这样就把K均值聚类的初始类选择问题,由主观确定变成了客观决定。
2、第二种方法
首先随机选择一个点作为第一个初始类中心点,然后计算该点与其他所有样本点的距离,选择距离最远的点作为第二个初始类的中心点,以此类推,直到选出K个初始类中心点。
(二)类别数K的确定
1、轮廓系数
轮廓系数(Silhouette Coefficient)可以用来判定聚类结果的好坏,也可以用来确定类别数K。好的聚类要保证类别内部样本之间的距离尽可能小(密集度),而类与类之间样本的距离尽可能大(离散度),轮廓系数就是一个用来度量类的密集度和离散度的综合指标。
轮廓系数的计算过程和使用如下:
①计算样本xi到同类Ck其他样本的平均距离ai,将ai称为样本xi的簇内不相似度,ai越小,说明样本xi越应该被分配到该类。
②计算样本xi到其他类Cj所有样本的平均距离bij,j=1, 2 ,..., K,j≠k,称为样本xi与类别Cj的不相似度。定义样本xi的簇间不相似度:bi =min{bi1, bi2, ...,bij,..., biK},j≠k,bi越大,说明样本xi越不属于其他簇。
③根据样本xi的簇内不相似度ai和簇间不相似度bi,定义样本xi的轮廓系数si,作为样本xi分类结果的合理性的度量。
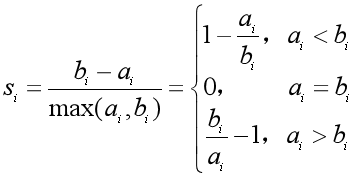
④轮廓系数范围在[-1,1]之间,该值越大,聚类结果越好。si接近1,则样本xi被分配到类别Ck的结果比较合理;si接近0,说明样本xi在两个类的边界上;si接近-1,说明样本xi更应该被分配到其他类别。
⑤计算所有样本的轮廓系数si的均值,得到聚类结果的轮廓系数S,作为聚类结果合理性的度量。轮廓系数越大,聚类结果越好。
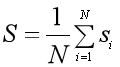
⑥使用不同的K值进行K均值聚类,计算各自聚类结果的轮廓系数S,选择较大的轮廓系数所对应的K值。
2、肘部法则
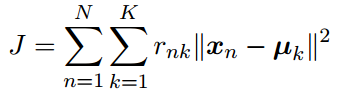
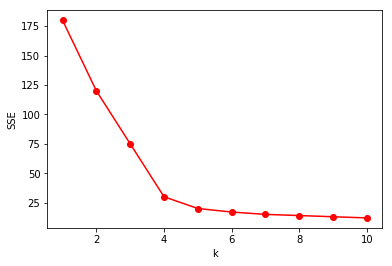
三、K均值聚类与高斯混合模型的关系
关于K均值聚类与EM算法、高斯混合模型的关系,主要有以下三点:
1、K均值聚类是一种非概率的聚类算法,属于硬聚类方法,也就是一个样本只能属于一个类(类与类之间的交集为空)。相比之下,高斯混合模型(GMM)是一种基于概率的聚类算法,属于软聚类方法,每个样本按照一个概率分布,属于多个类。
2、K均值聚类在一次迭代中的两个步骤,可以看做是EM算法的E步和M步,而且K均值聚类可以看做是用EM算法对⾼斯混合模型进行参数估计的⼀个特例,也就是高斯混合模型中分模型的方差σ2相等,为常数,且σ2→0时的极限情况。
3、K均值聚类和基于EM算法的高斯混合模型,对参数的初始化值比较敏感,由于K均值聚类的计算量远小于基于EM算法的高斯混合模型,所以通常运⾏K均值算法找到⾼斯混合模型的⼀个初始化值,再使用EM算法进行调节。具体而言,用K均值聚类划分的K个类别中,各类别中样本所占的比例,来初始化K个分模型的权重;用各类别中样本的均值来初始化K个高斯分布的期望;用各类别中样本的方差来初始化K个高斯分布的方差。
(一)从图形来理解
为了理解以上这几点,尤其是第2点,我们可以先从图形来看。假设高斯混合模型由4个高斯分布混合而成,高斯分布的密度函数如下。这里和《聚类之高斯混合模型与EM算法》的符号表示一致,y为样本。
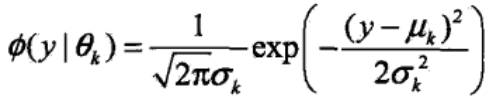
![]()
令均值μ=[0,2,4,6],方差σ2=[1,2,3,1],则4个高斯分布的概率密度函数的图形如下。我们可以看到,4个图形之间有重叠的部分,也就说明每个样本可以按照一个概率分布αk,属于多个类,只是属于某类的概率大些,属于其他类的概率小些。这表明高斯混合模型是一种软聚类方法。
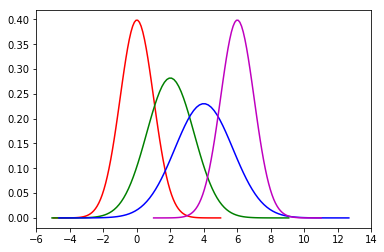
然后令均值μ不变,方差σ2=[0.01, 0.01, 0.01, 0.01],也就是4个分模型的方差σk2相等,而且σk2→0,那么4个高斯分布的图形如下。每个高斯分布的图形之间没有交集,那么每个样本只能属于一个类,变成了硬聚类。这也就是高斯混合模型的特例:K均值聚类。

(二)从公式来理解
用EM算法对高斯混合模型进行极大似然估计,在E步,我们需要基于第i轮迭代的参数θ(i)=(αk, μk, σk)来计算γjk,γjk是第j个样本yj来自于第k个高斯分布分模型的概率,k=1,2,...,K。在高斯混合模型中,γj是一个K维的向量,也就是第j个样本属于K个类的概率。假设分模型的方差σk2都相等,且是一个常数,不需要再估计,那么在EM算法的E步我们计算γjk

考虑σ2→0时的极限情况,如果样本yj属于第k类的概率最大,那么该样本与第k类的中心点的距离非常近,(yj - μk)2将会趋于0,于是有:
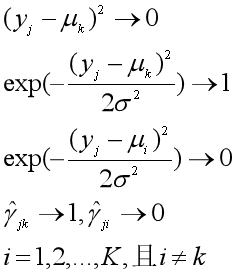
也就是样本yj属于第k类的概率近似为1,属于其他类别的概率近似为0,也就成为了一种硬聚类,也就是K均值聚类。
其实在σ2→0时的极限情况下,最大化高斯混合模型的完全数据的对数似然函数的期望,等价于最小化K均值聚类的目标函数J。
比如有4个高斯分布,样本yj的γj为[0.55, 0.15, 0.2, 0.1],那么属于第1类的概率γj1最大。而当分模型的方差σ2→0时,样本yj的γj可能为[0.98, 0.01, 0.005, 0.005],也就是该样本直接被分配到了第1类,成为了硬聚类。
附:4个高斯分布的概率密度函数的图形代码
import matplotlib.pyplot as plt import math import numpy as np # 均值 u1 = 0 u2 = 2 u3 = 4 u4 = 6 # 标准差 sig1 = math.sqrt(1) sig2 = math.sqrt(2) sig3 = math.sqrt(3) sig4 = math.sqrt(1) def x(u,sig): return np.linspace(u - 5*sig, u + 5*sig, 100) x1 = x(u1,sig1) x2 = x(u2,sig2) x3 = x(u3,sig3) x4 = x(u4,sig4) # 概率密度 def y(x,u,sig): return np.exp(-(x - u) ** 2 /(2* sig**2))/(math.sqrt(2*math.pi)*sig) y1 = y(x1,u1,sig1) y2 = y(x2,u2,sig2) y3 = y(x3,u3,sig3) y4 = y(x4,u4,sig4) plt.plot(x1,y1, "r-") plt.plot(x2, y2, "g-") plt.plot(x3, y3, "b-") plt.plot(x4, y4, "m-") plt.xticks(range(-6,16,2)) plt.show()
参考资料:
1、李航:《统计学习方法》(第二版)
2、《Pattern Recognition and Machine Learning》
3、https://www.jianshu.com/p/335b376174d4